概述
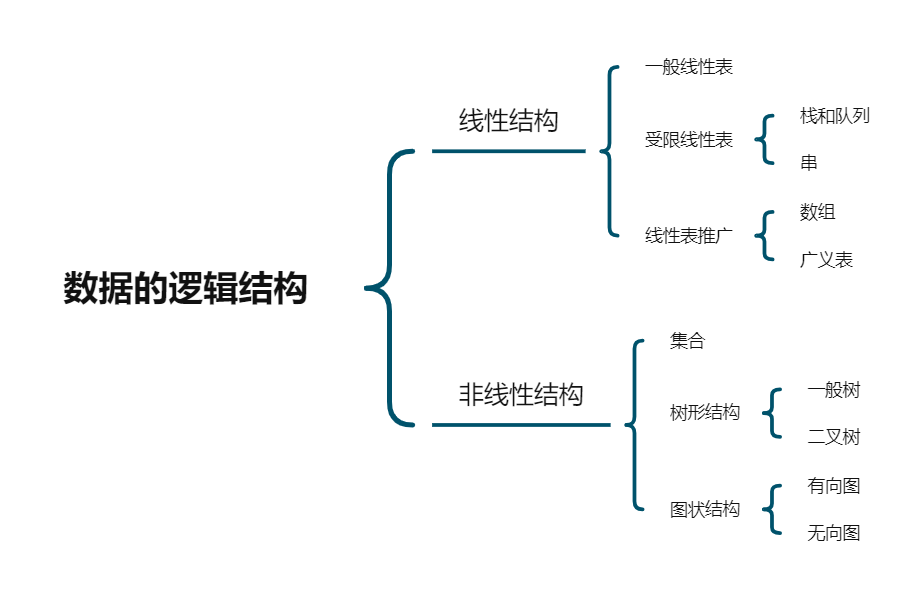
存储结构
- 顺序存储
- 链式存储
- 索引存储
- 散列存储
以下属于逻辑结构的是(
C)
A、顺序表 B、哈希表 C、有序表 D、单链表有序表是关键字有序的线性表,只描述逻辑以下与数据存储结构无关的术语是(
D)
A、循环队列 B、链表 C、哈希表 D、栈循环队列是顺序表表示的队列,而栈是抽象数据结构
在存储数据时,应该存储 1. 各个数据元素的值 2. 数据元素的关系
链式存储设计中,不同结点的存储空间可以不连续,但结点内的存储单元地址必须连续
推导时间复杂度
1 | int i = 1; |
找到正比的循环变量代入条件求解
设次数为$t$,则 $2^t \leq n $ —> $t \leq log_2{n}$
1 | int y=5; |
y+1的次数与$T(n)$成正比
设次数为$t$,则 $t = y - 5$
$(y+5+1)(t+5+1) < n$
$t < \sqrt{n-6}$
所以$T(n) = O(\sqrt{n})$
- 递归程序
$T(n) = 1 + T(n-1) = 1 + 1 + T(n-2) = …… = n -1 + T(1)$
所以$T(n) = O(n)$
树和二叉树
树的性质
- $结点数 = 结点度数 + 1$
- $度为 m 的树,第 i 层,至多m^{i-1}个结点$
- $高度为h的m叉树至多有\frac{m^h-1}{m-1}个结点$ ===> $1+2+3+4+5…$
- $具有n个结点的m叉树最小高度为\lceil\log_m{(n(m-1)+1)}\rceil$ ===> $ n\leq \frac{m^h-1}{m-1} $ ===> $h\geq\log_m{(n(m-1)+1)}$
二叉树的性质
- $叶子结点数等于度为2的结点数加1,即n_0 = n_2 + 1$
- $第k层至多2^{k-1}个结点$
- $高度为h,至多2^h-1个结点$
- $结点i所在的层次为\lfloor\log_2i\rfloor+1$
- $具有n个结点的完全二叉树高度为\lceil\log_2{(n+1)}\rceil或者是\lfloor\log_2n\rfloor+1$
$对于满m叉树,双亲结点为i号,则孩子结点第一个编号为j = (i-1)*m+2$
在二叉树中有2个结点,m和n,则使用(C)可以找到m到n的路径
A、先序 B、中序 C、后序 D、层次
线索二叉树是一种物理结构 ===> 加上了线索的链表结构
二叉树是逻辑结构
二叉树线索化后,仍不能有效求解的问题是(D)
A、先序线索二叉树中求先序后继
B、中序线索二叉树中求中序后继
C、中序线索二叉树中求中序前继
D、后续线索二叉树中求后序后继
$对于n个不同元素进栈,出栈序列个数为\frac{1}{n+1}C_{2n}^{n}$
$在m叉树的情况下,结点i的第一个子女编号为j = (i-1)*m+1$
$在m叉树的情况下,结点i的双亲的编号是\lfloor(i-2)/m\rfloor+1$
二叉树遍历的对应关系
图
有向图与无向图
$有向图: n个顶点,n(n-1)/2条边$
$无向图: n个顶点,n(n-1)条有向边$
邻接矩阵
- 对称且唯一
- 空间复杂度$O(n^2)$
- 对无向图而言:$第i行非零个数为第i个顶点的度$
- 对有向图而言:$第i行为出度的个数,第j列为入度的个数$
邻接表
- 存储空间
- 无向图:$O(|v|+2|e|)$
- 有向图:$O(|v|+|e|)$
- $顶点v在边表中出现次数为v的入度$
- $v的出度即为链表的长度$
- 不唯一
十字链表
- 对有向图而言
邻接多重表
- 对无向图而言
BFS(层序)
- $队列$
- $空间复杂度O(|v|)$
- $时间复杂度:$
- $邻接矩阵:O(|v|^2)$
- $邻接表:O(|v|+|E|)$
应用
最小生成树
$Prim–O(|v|^2)$
- 每次找两集合相连的边中的最小
- 适合稠密图
$Kruskal–O(|E|\log|E|)$
- 寻的边的权值是递增的
- 适合边稀疏,顶点较多的图
最短路径
单源最短路径:
- $Dijkstra:与Prim类似$
- $邻接矩阵O(|v|^2)$
- 不允许负值
每对顶点最短路径:
- $Floyd算法—O(|v|^3)$
- $每迭代一次,在从v_i到v_j的最短路径上就多考虑了一个顶点$
- 允许负权值,但不允许负权值组成回路
拓扑排序
- $每次选取入度为0的点$
- $O(|V|+|E|)$
- 邻接矩阵为三角阵,则存在拓扑排序,反之不成立
关键路径
AOE: 顶点表示事件,有向边表示活动
- 事件(点)最早发生时间:从前向后,最长
- 事件(点)最迟发生时间:从后向前,用最长减去最长
- 活动(边)最早开始时间:边前面的点的最早开始时间
- 活动(边)最迟开始时间:边后面的点的最迟时间与本身的权值之差
查找
顺序查找
一般线性表
ASL成功 $= \frac{1}{n}\frac{(n+1)n}{2} = \frac{n+1}{2}$
ASL不成功 $=n(n+1)\frac{1}{n} = n+1$有序表
ASL成功 $= \frac{n+1}{2}$
ASL不成功$=\frac{1+2+3+…+n+n}{n+1}= \frac{n}{2}+\frac{n}{n+1}$
折半查找
- ASL成功$=\frac{1}{n}(11+22+…+h2^{h-1})=\frac{n+1}{n}log_2{(n+1)}-1\approx log_2{(n+1)}-1$
- 查找不成功的次数至多为:$\lceil log_2{(n+1)}\rceil = \lfloor log_2n +1 \rfloor$
$失败结点个数*(所在层数-1)$ - $时间复杂度: O(log_2n)$
分块查找
- 块内无序,块间有序
- 第一步:顺序查找或折半查找索引表
第二步:块内顺序查找 - $若查找表长为n,分b块,每块S个记录,若均采用顺序查找,ASL = L_1+L_2=\frac{b+1}{2}+\frac{S+1}{2}= \frac{S^2+2S+n}{2S}$
$若块的长度=(总长度)^\frac{1}{2},即S=\sqrt{n},则ASL=\sqrt{n}+1$
$若索引表为折半查找,ASL = \lceil log_2{(b+1)} \rceil+ \frac{S+1}{2}$
B树和B+树
$m阶B树$
$各个结点子树个数x:$
$若为根,则2\leq x \leq m$
$若为非叶结点:则\lceil \frac{m}{2} \rceil \leq x \leq m$$各个结点关键字个数:$
$若为根,则1\leq x \leq m-1$
$若为非叶结点:则\lceil \frac{m}{2} \rceil -1 \leq x \leq m-1$$m阶B树, n个关键字,结点个数为k,高度为h$
$则 \lceil \frac{m}{2} \rceil ^ h -1 \leq k \leq \frac{m^h-1}{m-1}$
$log_m{(n+1)} \leq h \leq log_{\lceil \frac{m}{2} \rceil}{( \frac{n+1}{2} )}+1 $
$ (\lceil \frac{m}{2} \rceil -1 )(2^h-2) +1 \leq n \leq m^h-1$
$B+树$
- 非叶根结点(既不是叶结点也不是根结点)至少2棵子树,其他分支结点至少$\lceil \frac{m}{2} \rceil$个子树
- 结点子树个数与关键字个数相等
- $各个结点关键字个数x:$
$若为根:1 \leq x \leq m$
$若非根: \lceil \frac{m}{2} \rceil \leq x \leq m$ - 分支结点的某关键字为其子树中最大关键字的副本
散列表
- 冲突/碰撞不可避免
- ASL成功看关键字个数和冲突次数
ASL失败看表长
串
$’ababa’ 求next[]$
$’a’ 前缀:\emptyset 后缀:\emptyset \Longrightarrow \emptyset \bigcap \emptyset = \emptyset \Longrightarrow n = 0$
$’ab’ 前缀:{a} 后缀:{b} \Longrightarrow {a} \bigcap {b} = \emptyset \Longrightarrow n = 0 $
$’aba’ 前缀:{a,ab} 后缀:{a,ba}\Longrightarrow {a,ab} \bigcap {a, ba} = {a} \Longrightarrow n=1$
$’abab’ 前缀:{a,ab,aba} \bigcap 后缀:{b,ab,bab} = {ab} \Longrightarrow n=2$
$’ababa’ 前缀:{a,ab,aba,abab} \bigcap {a,ba,aba,baba} = {a,aba}\Longrightarrow n=3$
next数组有三种表示方法:
- $00123$
- $右移一位:(-1) 0012$
- $全部加一:01123$
排序
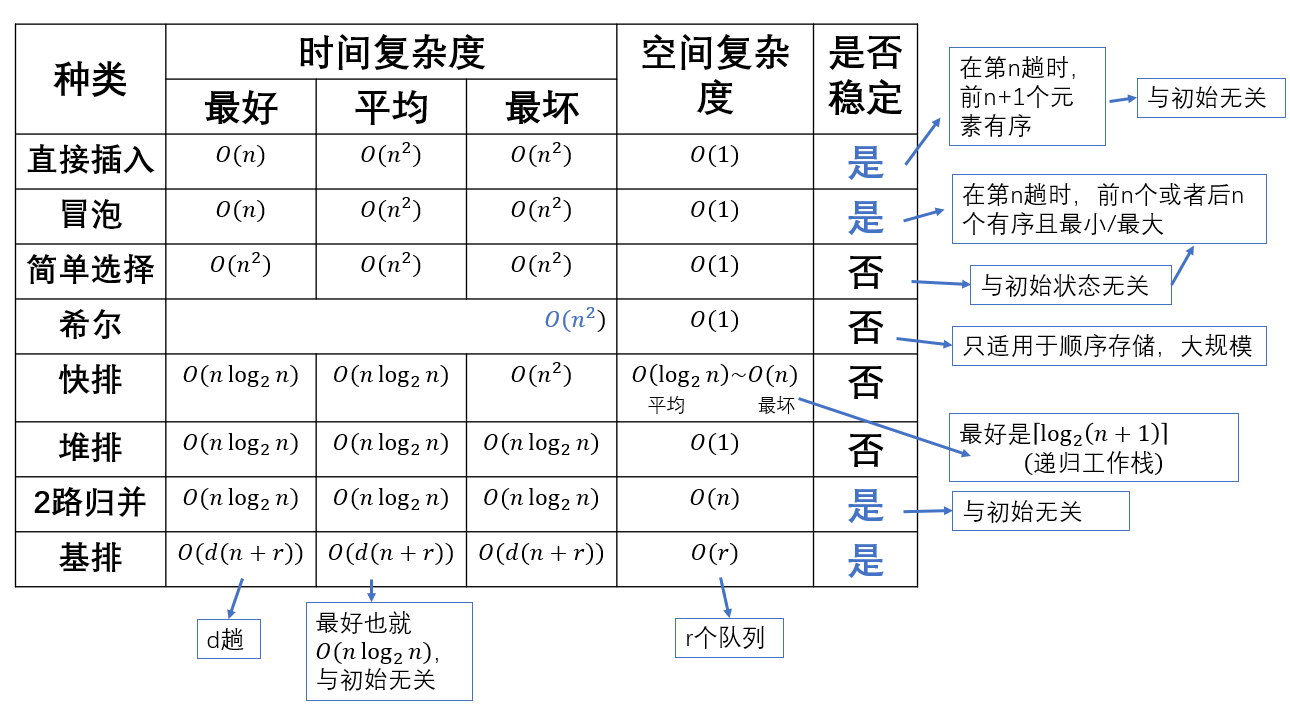
概念
- 同一线性表使用不用的排序方法,结果可能不同
- n个关键字基于比较的排序,两两比较次数至少为$\lceil log_2{(n!)} \rceil$
插入排序
基本有序,数据量不大
- 直接插入排序: 适用于顺序或者链式存储(边比较边移动)
- 折半插入排序: 先折半查找插入的位置,再移动,再插入,比较次数为$O(nlog_2n)$
- 希尔排序:
- $d_1 = \frac{n}{2} 并且 d_i=\lfloor \frac{d_{i-1}}{2} \rfloor$
- 各个组使用直接插入排序
- 重复迭代,直到$d_t = 1$
交换排序
冒泡排序
- 每次最小的元素放第一个位置
- 从后往前两两比较,若为逆序则交换
过程产生的有序子序列一定是全局有序的,这点与插入排序不同
快速排序
快排需要掌握算法
1 | void QuickSort(ElemType A[], int low, int hight) { |
选择排序
从前往后,每个元素与后面所有元素比较
简单选择
$移动次数: \leq 3(n-1) $
$比较次数: \frac{n(n-1)}{2}$
堆排序
- $构建时:对结点 \lfloor \frac{n}{2} \rfloor 一直到根的子树进行筛选$
- 排序:
- 输出堆顶,删除根节点
- 堆底送入根节点
- 自上而下调整,重复排序的第一步
- 插入:
- 结点插入到堆底
- 自下而上调整
归并与基排
归并排序
$对于N个元素,进行K路归并排序,趟数为m,则 K^m = N,所以m=\lceil log_k{N} \rceil$基数排序
- 最高位优先
- 最低位优先(推荐)
外部排序
$外部排序的总时间 = 内部排序时间 + 外存信息读写时间 + 内部归并时间$
$t_{es} = rt_{IS} + dt_{I/O}+S(n-1)t_{mg}$
$其中,r是初始归并段个数,d是外存访问次数,t_{I/O}是外存读写时间,S是归并趟数,(n-1)是记录数,t_{mg}是取关键字最小记录时间$在做m路平衡归并时,为实现输入/内部归并/输出的并行处理,要2m个输入缓冲区和2个输出缓冲区
$若一个2000记录文件,一个磁盘块250个记录,8个磁盘块,2路归并$
$则,2000/250 =8,即每趟8次读+8次写$
$归并段个数为8 ===> 内部排序 ===> 8+8次读写$
$S=\lceil log_m{r} = log_28 = 3 \rceil$
$所以读写次数为: 3(8+8) +8 + 8 = 64$
$所以,t_{es} = 8t_{Is}+64t_{I/O} + 3*2000t_{mg}$多路平衡归并与败者树
- $S趟归并共需比较次数:$
$S(n-1)(m-1) = \lfloor log_mr \rfloor (n-1)(m-1)= \frac{\lfloor log_2r \rfloor (n-1)(m-1)}{\lfloor log2m \rfloor}$ - 败者树:为了选出最小的元素
A、 大的为失败者,小的为胜利者
B、 非叶节点记录败者(较大的)比较时却比胜者(较小的) 置换-选择排序
- 生成初始归并段
- 长度不一时,使用哈夫曼树
工作区选择最小的元素就是使用败者树的
最佳归并树(采用哈夫曼树的思想)
记录数少的归并段先归并,总的I/O次数为2*(WPL)
$判断虚段数目x$
$n_0个归并段,m路归并$
$若(n_0-1)\%(m-1)=u \neq 0$
$则需要x=m-u-1个虚段$