前言
在 Leetcode 中学习了也有一阵子了,但是总感觉算法这玩意,时间一长就不熟练了,因此弄个学习笔记吧。用来记录一下在Leetcode的学习收获吧,也方便以后日后的复习。
这个学习笔记用来记录一些比较琐碎的知识,一些专题知识如果以后有时间再归纳汇总吧。
目前前的刷题进度如下: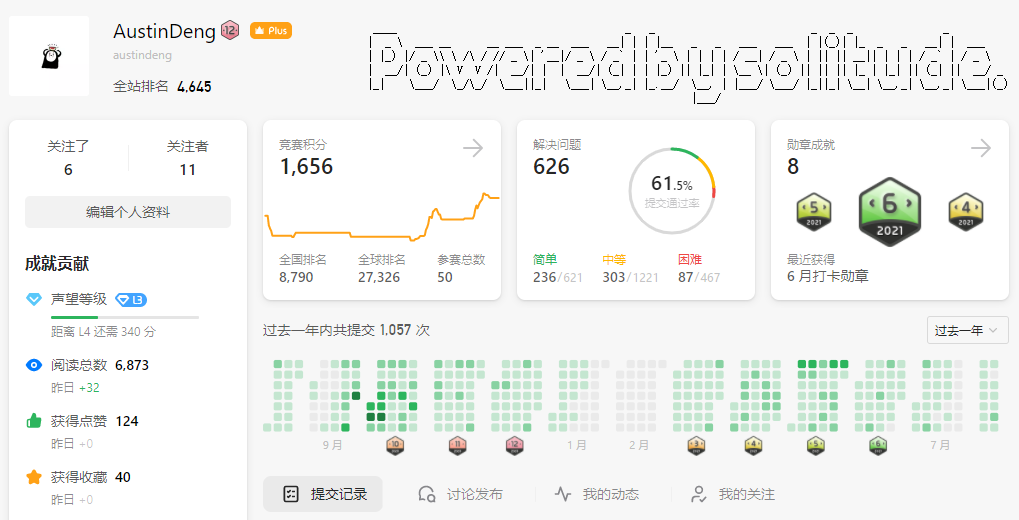
剑指office64:求1+2+3+…+n
求 1+2+...+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
示例一
输入: n = 3
输出: 6
实例二
输入: n = 9
输出: 45
限制
1 <= n <= 10000
逻辑运算符的短路性质
由于不能使用条件判断语句(A?B:C),因此我们可以使用逻辑运算符的短路性质来替代。
对于 A && B 这个表达式,如果 A 的判断为 $False$,那么 B 就不会执行;
同理 A || B 这个表达式,如果 A 的判断为 $True$,那么 B 就不会执行。
对于表达式 n == 0 ? 0 : n + sumNums(n - 1) 可以改写为 n && (n += sumNums(n-1))
俄罗斯农名乘法
考虑 A 和 B 两数相乘的时候利用加法和位运算来模拟.
其实就是将 B 二进制展开,如果 B 的二进制表示下第 $i$ 位为 1,那么这一位对最后结果的贡献就是 $A*(1<<i)$ ,即 $A<<i$。
遍历 B 二进制展开下的每一位,将所有贡献累加起来就是最后的答案。
这个方法经常被用于两数相乘取模的场景,如果两数相乘已经超过数据范围,但取模后不会超过,可以利用这个方法来拆位取模计算贡献,保证每次运算都在数据范围内。
1 | int quickMulti(int A, int B) { |
LRU 缓存机制
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制 。
实现 LRUCache 类:
- LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
- int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
- void put(int key, int value) 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
进阶:你是否可以在 O(1) 时间复杂度内完成这两种操作?
示例:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
提示:
- 1 <= capacity <= 3000
- 0 <= key <= 3000
- 0 <= value <= 104
- 最多调用 3 * 10^4 次 get 和 put
这道题主要运用到了双向链表以及哈希表的使用,注意怎么使用list的接口
1 | class LRUCache { |
5753. 有向图中最大颜色值
给你一个有向图,它含有n个节点和m条边。节点编号从0到n-1。
给你一个字符串colors,其中colors[i]是小写英文字母,表示图中第i个节点的颜色 (下标从 0 开始)。同时给你一个二维数组edges,其中edges[j] = [aj, bj]表示从节点aj到节点bj有一条有向边。
图中一条有效路径是一个点序列x1 -> x2 -> x3 -> ... -> xk,对于所有1 <= i < k,从xi到xi+1在图中有一条有向边。路径的颜色值是路径中出现次数最多颜色的节点数目。
请你返回给定图中有效路径里面的最大颜色值。如果图中含有环,请返回-1。
实例1: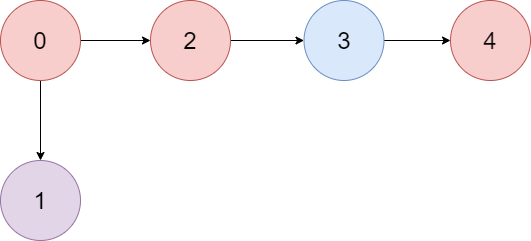
输入:colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
输出:3
解释:路径 0 -> 2 -> 3 -> 4 含有 3 个颜色为 "a" 的节点(上图中的红色节点)。
实例2: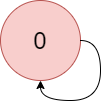
输入:colors = "a", edges = [[0,0]]
输出:-1
解释:从 0 到 0 有一个环。
提示:
我们需要求出的答案等价于:
对于一种颜色c, 以及一条路径path,其中颜色为c的节点有path_c个。我们希望挑选c以及path,使得path_c的值最大。
采用拓扑排序解题。
1 | class Solution { |
297. 二叉树的序列化与反序列化
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
示例1;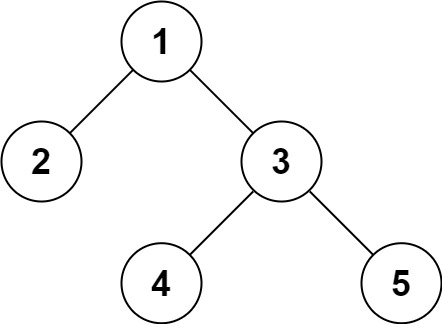
输入:root = [1,2,3,null,null,4,5]
输出:[1,2,3,null,null,4,5]
示例2:
输入:root = []
输出:[]
示例3:
输入:root = [1]
输出:[1]
提示:
- 树中结点数在范围 [0, 104] 内
- -1000 <= Node.val <= 1000
体会:
题目不是很难,关键在于反序列化。并且在序列化的过程中需要注意保留位置信息
第一次做这道题的时候,由于我的惯性思维:构造一棵二叉树至少需要两种遍历序列导致这题做了好久。思路是序列化的时候保存前序和中序序列,然后反序列化的时候通过前序和中序构造二叉树。GG。
1 | /** |
208. 实现 Trie (前缀树)
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。void insert(String word) 向前缀树中插入字符串 word 。boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
示例:
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
提示:
- 1 <=
word.length,prefix.length<= 2000 word和prefix仅由小写英文字母组成
1 | class Trie { |
1871. 跳跃游戏 VII
给你一个下标从 0 开始的二进制字符串 s 和两个整数 minJump 和 maxJump。一开始,你在下标 0 处,且该位置的值一定为 '0' 。
当同时满足如下条件时,你可以从下标 i 移动到下标 j 处:
i + minJump <= j <= min(i + maxJump, s.length - 1)且s[j] == '0'
如果你可以到达 s 的下标 s.length - 1 处,请你返回 true ,否则返回 false。
示例 1:
输入:s = "011010", minJump = 2, maxJump = 3
输出:true
解释:
第一步,从下标 0 移动到下标 3 。
第二步,从下标 3 移动到下标 5 。
示例 2:
输入:s = "01101110", minJump = 2, maxJump = 3
输出:false
提示:
2 <= s.length <= 105s[i]要么是'0',要么是'1's[0] == '0'1 <= minJump <= maxJump < s.length
思路:
使用 dp[i] 表示s在i这个位置上是否可达
dp[i] 是否可达取决于在下标[i-maxJump, i-minJump]这个区间中是否有可达的,即dp[j] == True, 其中i-maxJump <= j <= i-minJump
遍历[i-maxJump, i-minJump]一遍需要O(n)的时间复杂度,使用前缀和可以降低为O(1)
1 | class Solution { |
还有另外一种解法
使用滑动窗口+动态规划的思想,链接在此
50. Pow(x, n)
实现pow(x, n),即计算x的n次幂函数。
示例 1:
输入:x = 2.00000, n = 10
输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3
输出:9.26100
示例 3:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25
提示:
-100.0 < x < 100.0-231 <= n <= 231-1-104 <= xn <= 104
思路:
快速幂,可能解题的时候会用到,分为迭代和递归两种方法
1 | class Solution { |